14.5 DC Incident Energy Calculator (LEVEL 1)
Introduction
There have been several papers that have addressed the calculation of incident energy in direct current systems. Up to 2021, no standards that have the same standing as IEEE 1584, but it is likely that this will be addressed in coming years. That is of course, driven by the huge demand for calculations as DC systems become more abundant because of advances in solar and storage technology. Jim Phillips carried out research into the various methods and in 2010, introduced DC arc flash calculations into his Arc Flash courses as an addendum to his book, Arc Flash Calculation Studies. This was based upon 2 technical papers which were “Arc Flash Calculations for Exposures to DC Systems” by D.R. Doan and “DC Arc Models and Incident Energy Calculations” by R.F. Ammerman, T. Gammon, P.K. Sen and J.P. Nelson. Following on from Jim’s lead, these methods were introduced by commercial software companies. The calculator is based upon this method.
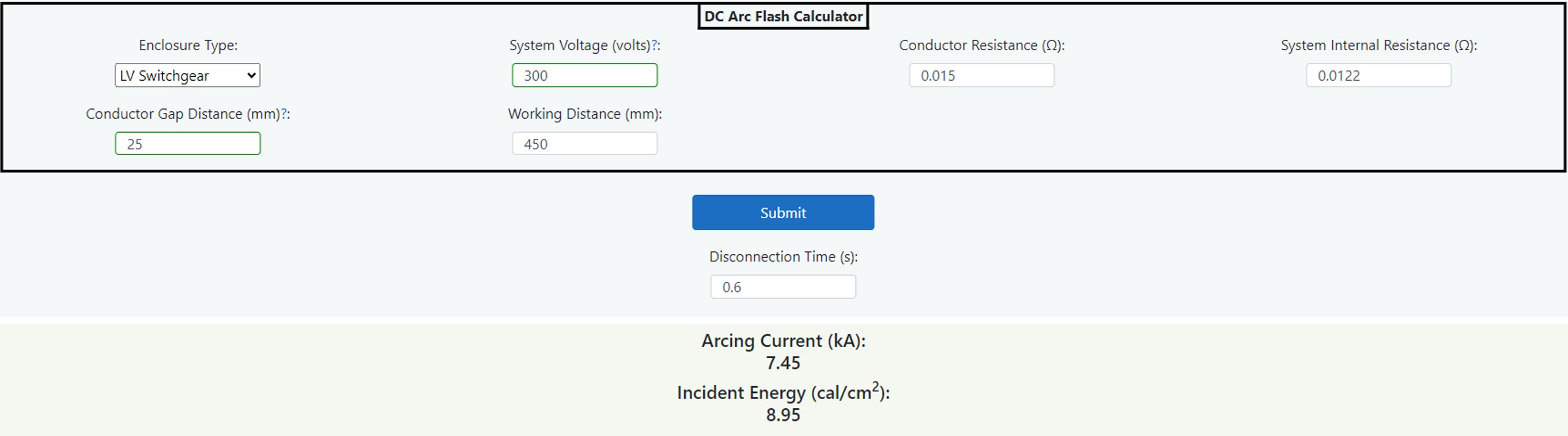
Figure 14.16 DC IE Calculator
Calculation method
If we take a simple DC circuit which is subject to an arc fault, the current that flows in the arc is found by application of ohms law which is I = V|R. So, the source voltage is divided by the sum of the series impedances made up of the; source resistance Rs, system (or conductor) resistance Rc and the arc resistance Rarc.
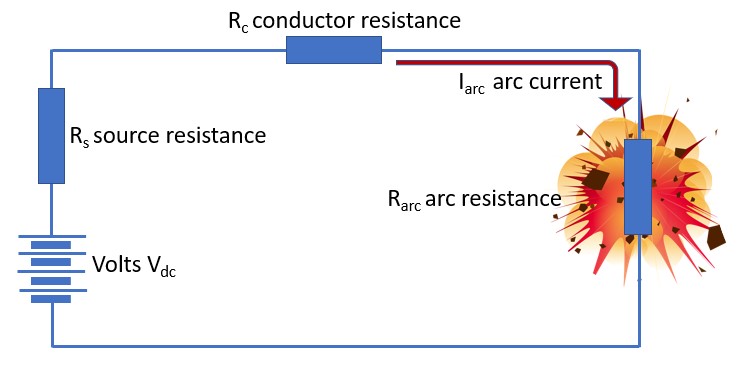
Figure 14.17 DC Circuit
To find the arc resistance Rarc we apply the following equation:
| Rarc = |
|
Where G = conductor gap in mm and Iarc = DC arcing current.
As can be seen we have two unknowns, Rarc and Idc_arc. It is necessary to apply an estimate of arcing current of 50% of the prospective short circuit current in order to get an estimate of arcing resistance Rarc. This is the voltage divided by the sum of Rc and Rs which gives us the prospective short circuit current multiplied by 50% giving the estimate of arcing current. This estimate is entered into the above equation to give a first arc resistance. This is added to the actual values of Rc and Rs which reveals a total estimated impedance which is divided into the voltage once more to determine a new value of arcing current. This new arcing current is used in the above equation and once again a new value of arc resistance is determined. This is repeated and through a process of iteration steps, the calculated values of both arcing current and arc resistance will get closer to the previous values until there is no significant difference.
The next stage in the calculation process is to find the arc energy Earc using the formulae: P = I2 x R x t watt/seconds using the calculated values for arcing current Idc_arc and arc resistance Rarc. The value t is the disconnection time of the circuit which is found by consulting the upstream protective device time current curve.
If the arc is in open air, the incident is found as follows:
| Ei air = |
|
cal/cm2 |
Where d is the distance measured from the arc source to the worker. This result is in cal/cm2